私は幼い頃から世の中のさまざまな現象に興味を持ちながら、勉強面では数学が好きで得意でした。ずっと「数学一筋」というわけではありませんでしたが、自分で考えて問題を解くことができたときの喜びは何よりのモチベーションになっていました。今も同じような感覚はありますが、世の中で起きているさまざまな現象を理解するために数学が役立つと感じてからは、現象を解明したいという新たなモチベーションも生まれました。

契機となったのは、チェコの大学院で修士論文を書き進めていた際に、植物の根が養分を吸収するプロセスのモデルを構築し、数学的に解析したことです。農業分野にも応用可能な知見が得られたのではないかと考えましたし、農学の研究者にコンタクトを取り、モデルの妥当性を聞いたこともありました。数学的には、モデルとなる偏微分方程式に対する初期値境界値問題の解の存在を証明したというのが修士論文のメインの結果でしたが、現象の解明のために、数学分野とは異なる幅広い分野と関わることのやりがいや面白さを感じた研究でもありました。

一方で私は、チェコにいるときから外国語の勉強が好きで、複数の外国語を学ぶ中の一つとして日本語を勉強していました。そして、高校時代にチャンスが訪れ、日本の山形県鶴岡市に半年間ホームステイで滞在しました。期間中は現地の高校に通って日本の高校生たちと触れ、さらに日本が気に入りましたし、後年になって進学のため再び来日してからも居心地がよく、現在に至っています。

ところで、数学には代数学・幾何学・解析学などがありますが、私がチェコのカレル大学在学中に専攻していたのは数値解析という分野です。数値解析は、問題をコンピュータで解くための方法を調べ、正しい解が出ることを証明していく学問です。例えば代数学は、天空の城を築くように抽象的な概念の探究に挑戦することが多いのですが、数値解析を含む解析学は現象とつながりやすく、具体的なイメージをしやすいところが私に合っていると感じました。もちろん幾何学も含めてそれぞれの分野にはつながりがありますが、純粋に数学の世界を掘り下げていくことに興味があるのか、実際の現象につながっているのが面白いと思うのかで、数学の研究を進めるモチベーションは人によって違うのかなと思います。私は数値解析や変分解析を軸とする解析学の世界に深入りしていき、植物の根の研究を起点にして、身の回りで起きている現象を、数学を通じて解明していく研究に力を入れるようになりました。

とはいえ、数学者である私が対象となる現象を見つけることは、そう簡単なことではありません。世の中に広くアンテナを向け、ニュースで見聞きしたものや、本で読んだこと、自然科学を扱う論文などに目を光らせるなど自ら情報収集を行うことも大切ですが、多くの人とコミュニケーションを重ねる中で課題が見つかることも少なくありません。私の場合は幸運なことに、異分野の方から「こういう課題があるが、数学的にアプローチできないか」と声を掛けていただくことがきっかけになることが多いです。私が来日した当時から、徐々に分野横断的で学際的な研究が盛んになり、今は欧米並みに活発になってきていると感じます。

私がこれまでにどのような現象の解明に挑んできたかというと、まずは「液滴の運動」です。液滴とは、何らかの物体からしたたり落ちる液体の粒であり、これが重力で滑り落ちる現象を解析しました。その後、細胞組織のパターンが形成されるプロセスの解析や、マグネシウム合金の性質を向上させるための研究などにも挑み、これらのテーマは現在も研究を続けています。

ここでは、「コルチ器」の細胞パターンに関するテーマについて簡単に紹介します。コルチ器とは耳の中にある感覚器官で、音を感知する機能を持つ重要な器官です。その内部では、「有毛細胞」と「支持細胞」という2種類の細胞が、サッカーボールの模様に近い、幾何学的な美しいパターンを形成しています。この2種類の細胞は、胚ができてからしばらくはランダムに散らばっていますが、あるタイミングで規則正しい市松模様に配列し、最終的にサッカーボール模様に並んでいきます。健康な個体であれば、どの個体でもほぼ同じタイミングで同じようなパターンを作ります。まるで何かによって操作されているような2種類の細胞の動きが、自然に、そして安定的に起きるメカニズムはわかっていませんでした。このメカニズムの解明に取り組んでいた生物学者のグループは「2種類の細胞同士の接着力が細胞の種類や時間によって変化することで、規則的な細胞の配列が起きているのではないか」という仮説を持っていました。この仮説を実験だけで証明することは非常に困難だったことから、彼らは私たち数学者とタッグを組むことにしたのです。共同研究の末、仮説をベースに私たちが検討したシミュレーションの結果と、生物学者が実験を通じて提示した実際のコルチ器上皮の写真とで、それぞれのタイミングにおける「有毛細胞」と「支持細胞」の配列が見事に一致しました。コルチ器上皮での特徴的な細胞配列は、細胞の接着力により駆動されることを解明できたのです。

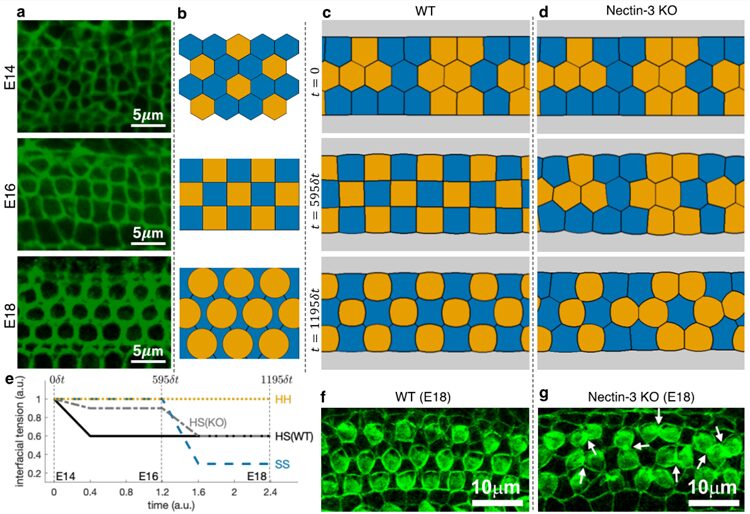
マウスの胚ができてから14日目（E14）、16日目（E16）、18日目（E18）のコルチ器内の聴覚上皮の写真（a列, f, g）、その模式図（b列）と、それぞれのタイミングで測定した細胞同士の接着力（e）をパラメータに代入して得られたシミュレーション結果の比較（c列：健康なマウス、d列：接着分子を阻害したマウス）。黄色が「有毛細胞」、青が「支持細胞」を表す。
※R. Z. Mohammad, H. Murakawa, K. Svadlenka, H. Togashi, A numerical algorithm for modeling cellular rearrangements in tissue morphogenesis, Communications Biology 5, 239 (2022)より引用

先ほどのプロジェクトではまず、生物学者が立てていた仮説を基に、細胞の集まりが持つエネルギーを細胞同士の接着力を使って数式化し、「この数式の極小値に対応して細胞が配列している」という数理モデルを考えました。ただし、この数式をそのままコンピュータに預ければ解を出してくれるわけではありません。まず、このモデルに解が存在するかを保証する必要があります。「この数式は、この条件の下であれば、この範囲に必ず解がある」ということがわかっていないと、コンピュータの計算結果が私たちの求めていた解なのかを判断することができないのです。それが確認出来たら、次はコンピュータが正確に、確実に計算できるような近似法を考えます。今回考えた数式は無限次元ですが、コンピュータは有限次元しか扱うことができませんので、次元を落とすという作業（近似）が必要です。精度はもちろんですが、計算に時間がかかりすぎないよう効率性も意識した近似法を検討しなければなりません。

このようなプロセスの間には、複雑な現象に影響を及ぼしている多種多様な要素の中から、数理モデル化においては重要ではない要素を取り除く「粗視化」という作業が不可欠です。また、実験では確認できない要素を数式のパラメータとして使ったり、あまりに多くのパラメータが入った数式でモデルを作ったりしてしまうと、信ぴょう性の低いシミュレーション結果になってしまう可能性があります。その現象のどんな部分をどのスケールで見たいのかを整理しながら共同研究者と何度もディスカッションを重ね、数学的な視点と異分野の視点を行ったり来たりしながら、最適な粗視化・数理モデル化を検討していくのです。これは非常に難しいプロセスですが、異分野の研究者と共同で研究することでしか体験できない、ワクワクする経験でもあります。

こうした共同研究は、数学が実際の世界とつながることを実感できるやりがいのある取り組みであることは間違いありませんが、注意が必要なポイントがあります。それは、数学者の立場からすると、現象を理解すること自体が最終的なゴールではないということです。数学者が目指すのは、現象の理解に必要となる「数学の新たな知見や法則などを導き出す」こと。数学者なら誰もが知っているような数学理論を使い、既存の数学的なアプローチによって何らかの現象が解明できたとしても、数学者として十分な研究成果を得られたとは言えません。例えば、先ほど紹介したコルチ器の細胞パターンのテーマでは、新たな理論を使った近似法を提案したところが数学的な研究成果でした。数理モデルは比較的簡単なものでしたが、既存の近似法ではコンピュータでうまく計算することができなかったのです。数学的な研究成果を得られたことが、結果的に細胞配列のメカニズム解明につながった、というポイントは、私たち数学者がこの共同研究に参加した大きな意義だったと思います。

数学者は、定量化できるものを対象とした幅広い分野で、現象の解明に寄与する様々な成果をあげています。ある数学者は流体力学の理論や流体の方程式を駆使して、気候変動に関連する研究を進めています。経済学の数理ファイナンスという分野では、社会の経済動向を数学的に解析しようとする数学者もいます。私自身はというと、先ほど挙げた3つのテーマのほか、近年は界面現象に興味があり、例えば化学反応などにより時間とともに変化していく環境に合わせて界面が動く現象を解析していきたいと考えています。また東京都立大学では、生命科学、化学、物理学、生体材料科学など、様々な分野の研究者が集まって医学領域のテーマについて議論する研究チームがあり、私も参加しています。ゆくゆくは、そのメンバーでも共同研究ができたら嬉しいですね。

私の研究室には、現象を数学で表すことに興味がある学生がいれば、純粋な変分解析に興味を示す学生もいます。どんな研究テーマであっても、最終的な目的は私の研究と同様に「数学的な成果を出す」ことです。使用するのは既存のモデル方程式でも構いませんが、解が存在することを明らかにしたり、解の満たす性質を見つけたりと、これまで数学的にわかっていなかったことを新たな考え方で解明することが求められます。

ここまで読んで、現象を数学で解明することに興味を持ってくれた方がいたらとてもうれしいことですが、修士の学位を取るまでは現象の解明よりも「数学の知識をしっかりと身につけ、数学的な成果を出す」ことに集中する必要があるだろうと思います。遠い道のりのように感じるかもしれませんが、先ほど紹介したように、学際的な共同研究に数学者が参加したからこそ生み出せる成果は、この時間なくしては得られません。とはいえ、「現象を数学で解明する現場を身近に感じたい」と思う学生は、私の共同研究者とのディスカッションやラボ見学に同席してもらって、その現場を体験してもらうことは可能です。皆さんが自らの手で、これまでの数学では解明できなかった現象を明らかにしてくれる日を楽しみにしています。